Feynman Tekniği
Feynman Tekniği
Bir şeyi gerçekten öğrenmek istiyorsanız onu beş yaşındaki bir çocuğa anlatabilecek basitlikte, öğrenmeniz ve derinlemesine kavramanız gerekmektedir. Bir konuyu başkalarına açıklayabilmek için hem o konuyu anlamalı, hem de anlamamanın nasıl olduğunu kavramanız gerekmektedir.
Ercan Caner, Sun Savunma Net, 14 Temmuz 2024
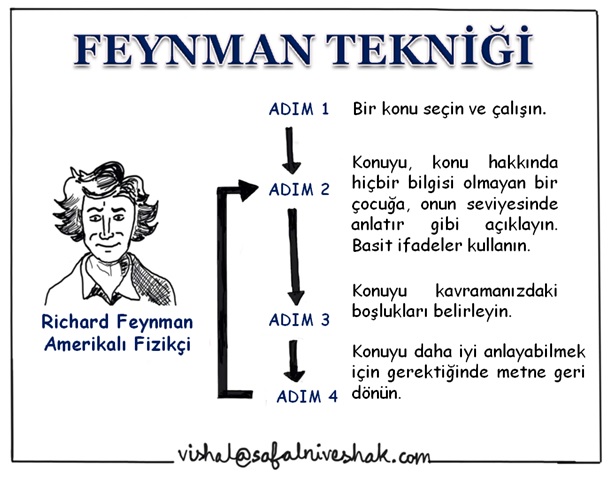
Richard Feynman 1918 yılında ABD’nin New York eyaletinde Queens’teki Far Rockway adlı küçük bir kasabada dünyaya gelmiştir. Henüz 16 yaşındayken türev ve integral hesabını bütün yönleriyle kavrayan Feynman, 17 yaşında Rockway’den ayrılıp, lisans derecesini yapacağı MIT (Massachusetts Institute of Technology)’e girmiştir. Lisans derecesinden sonra Princeton Üniversitesi’ne kabul edilen ve doktorasını tamamlayan Feynman, 1942 yılında ABD’nin savaşa katılmasıyla birlikte, Manhattan Projesi’nde çalışmak üzere çağrılmıştır.
Sadece 20 yaşındayken, 1942-1945 yılları arasında ilk atom bombasını imal etmek üzere Manhattan Projesinde çalışan Nobel ödüllü fizikçi Richard Feynman, öğrenmenin temelinin basitlik olduğuna inanmaktadır. Feynman 1965 yılında kuantum elektrodinamik alanındaki çalışmalarıyla Julian Schwinger ve Sin-Itiro Tomonaga ile Nobel Ödülü’nü kazanmıştır.
Feynman, öğrenmenin temelinin basitlikte yattığını ve basitleştikçe öğrenme ve akılda tutmanın kolaylaştığına inanmaktadır. Ona göre karmaşık açıklamalar ve ifadelerle dolu bilginin kavranma olasılığı çok azdır. Öğrenmenin amacı dünyayı daha iyi anlamaktır, ancak öğrenme şeklimiz çoğunlukla bunu sağlamaktan çok uzaktır.
Bir konu, kitaptaki şekliyle ya da öğretmenin anlattığı şekilde ezberlendiğinde çok geçmeden unutulması kaçınılmazdır. İşte burada Feynman Tekniği devreye girmektedir. Feynman Tekniğinin temeli bir şeyi herkesin anlayabileceği şekilde basitleştirmektir. Böyle yapılarak çalışılan konu derinlemesine öğrenilebilir. Feynman Tekniğinin dört aşaması bulunmaktadır.
- Bir konu belirleyin ve çalışmaya başlayın
Feynman tekniği sadece matematik veya fizikte geçerli değildir, bu teknik her şeye uygulanabilir. Öğrenmek istediğiniz bir konuyu seçin ve boş bir kâğıda yazın. Boş kâğıt, her şeye sıfırdan başladığınızı kabullenmeniz anlamına gelir. Unutmayın en önemli prensip kendinizi kandırmamaktır ve kandırılması en kolay kişi kendinizdir.
- Konuyu kendinize veya bir çocuğa açıklayın
Bu adım sizin çalıştığınız konuyu öğrenip öğrenmediğinizi belirlemenizi sağlayacaktır. Konsepti kendi ifadenizle tercihen beş yaşındaki bir çocuğa öğretecek şekilde açıklayın. Meseleleri basit kelimelerle parçalara böldüğünüzde o konu hakkında yeterli bilgiye sahip olup olmadığınızı anlayabilirsiniz. Bu öğrenmenizdeki boşlukları da kavramanıza neden olacaktır.
- Tıkandığınızda çalışma dokümanına geri dönün
Bir konuyu basit ifadelerle açıklayabildiğinizde onu tamamen anlamış olacaksınız. Bu; öğrendiklerinizin sonsuza kadar size yapışacağı ve onları asla unutmayacağınız anlamına gelmektedir ve ezberlemekten tamamen farklıdır. Aldığınız notları, hâlâ anlamadığınız hususların olup olmadığını belirlemek için gözden geçirin. Ve kendinize anlatmayı deneyin. Eğer çok zor ise veya bir kitaptan alıntı ifadeler kullanmak zorunda kalıyorsanız hâlâ meselenin özünü kavrayamamışsınızdır.
- Düzenleyin ve gözden geçirin
Doğal ve basit bir açıklama yapana kadar devam edin. İhtiyaç duyduğunuzda 2 ve 3 numaralı adımlara istediğiniz kadar geri dönebilirsiniz. Merak etmeyin, sandığınız kadar uzun sürmeyecektir.
Örnekli Anlatım-İntegral
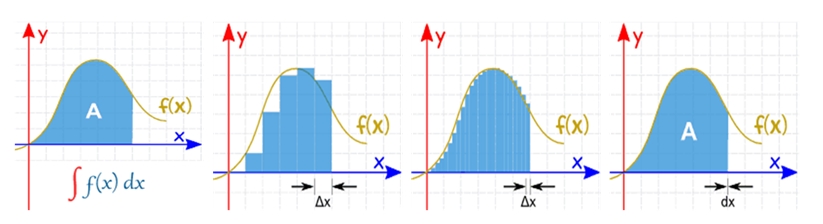
İntegral bir fonksiyon grafiğinin altındaki alanı bulmak için kullanılan sayısal bir yöntemdir, belli bir değerin, belli bir diğer değere göre değişiminin toplamıdır. Bir f(x) fonksiyonun integrali en soldaki grafikte görülen eğrinin altında kalan mavi renkli ‘‘A’’ alanıdır. Gerçekte de integral kelimesinin anlamı parçalardan oluşmuş bir bütün demektir. Peki, integral hakkında hiçbir şey bilmiyorsanız bu alanı nasıl hesaplayabilirsiniz?
En basit yöntem mavi renkle gösterilen ‘‘A’’ alanının ince dikdörtgenlere bölmek ve hepsinin alanlarını toplamaktır. Neden mi dikdörtgene bölüyoruz? Çünkü dikdörtgenlerin alanını hesaplamak kolaydır.
Yukarıda soldan ikinci grafiğe baktığımızda bunun yaklaşık alan olduğunu görebiliriz, nedeni de bazı noktalarda dikdörtgenler eğrinin dışına taşarken bazı noktalarda da eğrinin altında kalmaktadır.
Gerçeğe en yakın alan değerini bulmak istiyorsak dikdörtgenleri incelterek sayısını artırabiliriz.
Dilimlerin genişliği sıfıra yaklaştıkça (dx) gerçek alan bilgisine ulaşırız.
Ve integral; bütün bu dilimleri, genişlikleri sıfıra yaklaştığında toplama yöntemidir.
Unutmayın! Öğrenmek ve bir daha asla unutmayacak şekilde derinlemesine bir konuyu kavramak istiyorsanız, o konuyu beş yaşındaki bir çocuğa basit ifadelerle anlatabilecek hale gelmek zorundasınız.